Одна из самых сложных тем для учащихся – это решение уравнений, содержащих переменную под знаком модуля. Давайте разберемся для начала с чем же это связано? Почему, например, квадратные уравнения большинство детей щелкает как орешки, а с таким далеко не самым сложным понятием как модуль имеет столько проблем?

На мой взгляд, все эти сложности связаны с отсутствием четко сформулированных правил для решения уравнений с модулем. Так, решая квадратное уравнение, ученик точно знает, что ему нужно сначала применять формулу дискриминанта, а затем формулы корней квадратного уравнения. А что делать, если в уравнении встретился модуль? Постараемся четко описать необходимый план действий на случай, когда уравнение содержит неизвестную под знаком модуля. К каждому случаю приведем несколько примеров.

Но для начала вспомним определение модуля . Итак, модулем числа a называется само это число, если a неотрицательно и -a , если число a меньше нуля. Записать это можно так:

|a| = a, если a ≥ 0 и |a| = -a, если a < 0

Говоря о геометрическом смысле модуля, следует помнить, что каждому действительному числу соответствует определенная точка на числовой оси – ее координата. Так вот, модулем или абсолютной величиной числа называется расстояние от этой точки до начала отсчета числовой оси. Расстояние всегда задается положительным числом. Таким образом, модуль любого отрицательного числа есть число положительное. Кстати, даже на этом этапе многие ученики начинают путаться. В модуле может стоять какое угодно число, а вот результат применения модуля всегда число положительное.

Теперь перейдем непосредственно к решению уравнений.

1. Рассмотрим уравнение вида |x| = с, где с – действительное число. Это уравнение можно решить с помощью определения модуля.

Все действительные числа разобьем на три группы: те, что больше нуля, те, что меньше нуля, и третья группа – это число 0. Запишем решение в виде схемы:

{±c, если с > 0

Если |x| = c, то x = {0, если с = 0

{нет корней, если с < 0

1) |x| = 5, т.к. 5 > 0, то x = ±5;

2) |x| = -5, т.к. -5 < 0, то уравнение не имеет корней;

3) |x| = 0, то x = 0.

2. Уравнение вида |f(x)| = b, где b > 0. Для решения данного уравнения необходимо избавиться от модуля. Делаем это так: f(x) = b или f(x) = -b. Теперь необходимо решить отдельно каждое из полученных уравнений. Если в исходном уравнении b< 0, решений не будет.

1) |x + 2| = 4, т.к. 4 > 0, то

x + 2 = 4 или x + 2 = -4

2) |x 2 – 5| = 11, т.к. 11 > 0, то

x 2 – 5 = 11 или x 2 – 5 = -11

x 2 = 16 x 2 = -6

x = ± 4 нет корней

3) |x 2 – 5x| = -8 , т.к. -8 < 0, то уравнение не имеет корней.

3. Уравнение вида |f(x)| = g(x). По смыслу модуля такое уравнение будет иметь решения, если его правая часть больше или равна нулю, т.е. g(x) ≥ 0. Тогда будем иметь:

f(x) = g(x) или f(x) = -g(x) .

1) |2x – 1| = 5x – 10. Данное уравнение будет иметь корни, если 5x – 10 ≥ 0. Именно с этого и начинают решение таких уравнений.

1. О.Д.З. 5x – 10 ≥ 0

2. Решение:

2x – 1 = 5x – 10 или 2x – 1 = -(5x – 10)

3. Объединяем О.Д.З. и решение, получаем:

Корень x = 11/7 не подходит по О.Д.З., он меньше 2, а x = 3 этому условию удовлетворяет.

Ответ: x = 3

2) |x – 1| = 1 – x 2 .

1. О.Д.З. 1 – x 2 ≥ 0. Решим методом интервалов данное неравенство:

(1 – x)(1 + x) ≥ 0

2. Решение:

x – 1 = 1 – x 2 или x – 1 = -(1 – x 2)

x 2 + x – 2 = 0 x 2 – x = 0

x = -2 или x = 1 x = 0 или x = 1

3. Объединяем решение и О.Д.З.:

Подходят только корни x = 1 и x = 0.

Ответ: x = 0, x = 1.

4. Уравнение вида |f(x)| = |g(x)|. Такое уравнение равносильно двум следующим уравнениям f(x) = g(x) или f(x) = -g(x).

1) |x 2 – 5x + 7| = |2x – 5|. Данное уравнение равносильно двум следующим:

x 2 – 5x + 7 = 2x – 5 или x 2 – 5x +7 = -2x + 5

x 2 – 7x + 12 = 0 x 2 – 3x + 2 = 0

x = 3 или x = 4 x = 2 или x = 1

Ответ: x = 1, x = 2, x = 3, x = 4.

5. Уравнения, решаемые методом подстановки (замены переменной). Данный метод решения проще всего объяснить на конкретном примере. Так, пусть дано квадратное уравнение с модулем:

x 2 – 6|x| + 5 = 0. По свойству модуля x 2 = |x| 2 , поэтому уравнение можно переписать так:

|x| 2 – 6|x| + 5 = 0. Сделаем замену |x| = t ≥ 0, тогда будем иметь:

t 2 – 6t + 5 = 0. Решая данное уравнение, получаем, что t = 1 или t = 5. Вернемся к замене:

|x| = 1 или |x| = 5

x = ±1 x = ± 5

Ответ: x = -5, x = -1, x = 1, x = 5.

Рассмотрим еще один пример:

x 2 + |x| – 2 = 0. По свойству модуля x 2 = |x| 2 , поэтому

|x| 2 + |x| – 2 = 0. Сделаем замену |x| = t ≥ 0, тогда:

t 2 + t – 2 = 0. Решая данное уравнение, получаем, t = -2 или t = 1. Вернемся к замене:

|x| = -2 или |x| = 1

Нет корней x = ± 1

Ответ: x = -1, x = 1.

6. Еще один вид уравнений – уравнения со «сложным» модулем. К таким уравнениям относятся уравнения, в которых есть «модули в модуле». Уравнения данного вида можно решать, применяя свойства модуля.

1) |3 – |x|| = 4. Будем действовать так же, как и в уравнениях второго типа. Т.к. 4 > 0, то получим два уравнения:

3 – |x| = 4 или 3 – |x| = -4.

Теперь выразим в каждом уравнении модуль х, тогда |x| = -1 или |x| = 7.

Решаем каждое из полученных уравнений. В первом уравнении нет корней, т.к. -1 < 0, а во втором x = ±7.

Ответ x = -7, x = 7.

2) |3 + |x + 1|| = 5. Решаем это уравнение аналогичным образом:

3 + |x + 1| = 5 или 3 + |x + 1| = -5

|x + 1| = 2 |x + 1| = -8

x + 1 = 2 или x + 1 = -2. Нет корней.

Ответ: x = -3, x = 1.

Существует еще и универсальный метод решения уравнений с модулем. Это метод интервалов. Но мы его рассмотрим в дальнейшем.

blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Модуль числа a — это расстояние от начала координат до точки А (a ).

Чтобы понять это определение, подставим вместо переменной a любое число, например 3 и попробуем снова прочитать его:

Модуль числа 3 — это расстояние от начала координат до точки А (3 ).

Становится ясно, что модуль это ни что иное, как обычное расстояние. Давайте попробуем увидеть расстояние от начала координат до точки А(3 )

Расстояние от начала координат до точки А(3 ) равно 3 (трём единицам или трём шагам).

Модуль числа обозначает двумя вертикальными линиями, например:

Модуль числа 3 обозначается так: |3|

Модуль числа 4 обозначается так: |4|

Модуль числа 5 обозначается так: |5|

Мы искали модуль числа 3 и выяснили, что он равен 3. Так и записываем:

Читается как: «Модуль числа три равен три»

Теперь попробуем найти модуль числа -3. Опять же возвращаемся к определению и подставляем в него число -3. Только вместо точки A используем новую точку B . Точку A мы уже использовали в первом примере.

Модулем числа —3 называют расстояние от начала координат до точки B (—3 ).

Расстояние от одного пункта до другого не может быть отрицательным. Поэтому и модуль любого отрицательного числа, будучи являясь расстоянием тоже не будет отрицательным. Модуль числа -3 будет число 3. Расстояние от начала координат до точки B(-3) равно также трём единицам:

Читается как: «Модуль числа минус три равен три»

Модуль числа 0 равен 0, та как точка с координатой 0 совпадает с началом координат, т.е. расстояние от начала координат до точки O(0) равно нулю:

«Модуль нуля равен нулю»

Делаем выводы:

• Модуль числа не может быть отрицательным;
• Для положительного числа и нуля модуль равен самому числу, а для отрицательного – противоположному числу;
• Противоположные числа имеют равные модули.

Противоположные числа

Числа, отличающиеся только знаками называют противоположными . Например, числа −2 и 2 являются противоположными. Они отличаются только знаками. У числа −2 знак минуса, а у 2 знак плюса, но мы его не видим, потому что плюс, как мы говорили ранее, по традиции не пишут.

Еще примеры противоположных чисел:

Противоположные числа имеют равные модули. Например, найдём модули для −2 и 2

На рисунке видно, что расстояние от начала координат до точек A(−2) и B(2) одинаково равно двум шагам.

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Не мы выбираем математику своей профессией, а она нас выбирает.

Российский математик Ю.И. Манин

Уравнения с модулем

Наиболее сложно решаемыми задачами школьной математики являются уравнения, содержащие переменные под знаком модуля. Для успешного решения таких уравнений необходимо знать определение и основные свойства модуля. Естественно, что учащиеся должны иметь навыки решения уравнений такого типа.

Основные понятия и свойства

Модуль (абсолютная величина) действительного числа обозначается и определяется следующим образом:

К простым свойствам модуля относятся следующие соотношения:

Отметим , что последние два свойства справедливы для любой четной степени.

Кроме того , если , где , то и

Более сложные свойства модуля , которые можно эффективно использовать при решении уравнений с модулями , формулируются посредством следующих теорем:

Теорема 1. Для любых аналитических функций и справедливо неравенство

Теорема 2. Равенство равносильно неравенству .

Теорема 3. Равенство равносильно неравенству .

Рассмотрим типовые примеры решения задач на тему «Уравнения , содержащие переменные под знаком модуля».

Решение уравнений с модулем

Наиболее распространенным в школьной математике методом решения уравнений с модулем является метод , основанный на раскрытии модулей. Этот метод является универсальным , однако в общем случае его применение может привести к весьма громоздким вычислениям. В этой связи учащиеся должны знать и другие , более эффективные методы и приемы решения таких уравнений. В частности , необходимо иметь навыки применения теорем , приведенных в настоящей статье.

Пример 1. Решить уравнение . (1)

Решение. Уравнение (1) будем решать «классическим» методом –методом раскрытия модулей. Для этого разобьем числовую ось точками и на интервалы и рассмотрим три случая.

1. Если , то , , , и уравнение (1) принимает вид . Отсюда вытекает . Однако здесь , поэтому найденное значение не является корнем уравнения (1).

2. Если , то из уравнения (1) получаем или .

Так как , то корень уравнения (1).

3. Если , то уравнение (1) принимает вид или . Отметим , что .

Ответ: , .

При решении последующих уравнений с модулем будем активно использовать свойства модулей с целью повышения эффективности решения подобных уравнений.

Пример 2. Решить уравнение .

Решение. Так как и , то из уравнения следует . В этой связи , , , и уравнение принимает вид . Отсюда получаем . Однако , поэтому исходное уравнение корней не имеет.

Ответ: корней нет.

Пример 3. Решить уравнение .

Решение. Так как , то . Если , то , и уравнение принимает вид .

Отсюда получаем .

Пример 4. Решить уравнение .

Решение. Перепишем уравнение в равносильном виде . (2)

Полученное уравнение относится к уравнениям типа .

Принимая во внимание теорему 2, можно утверждать, что уравнение (2) равносильно неравенству . Отсюда получаем .

Ответ: .

Пример 5. Решить уравнение .

Решение. Данное уравнение имеет вид . Поэтому , согласно теореме 3 , здесь имеем неравенство или .

Пример 6. Решить уравнение .

Решение. Положим , что . Так как , то заданное уравнение принимает вид квадратного уравнения , (3)

где . Поскольку уравнение (3) имеет единственный положительный корень и , то . Отсюда получаем два корня исходного уравнения: и .

Пример 7. Решить уравнение . (4)

Решение. Так как уравнение равносильно совокупности двух уравнений: и , то при решении уравнения (4) необходимо рассмотреть два случая.

1. Если , то или .

Отсюда получаем , и .

2. Если , то или .

Так как , то .

Ответ: , , , .

Пример 8. Решить уравнение . (5)

Решение. Так как и , то . Отсюда и из уравнения (5) следует, что и , т.е. здесь имеем систему уравнений

Однако данная система уравнений является несовместной.

Ответ: корней нет.

Пример 9. Решить уравнение . (6)

Решение. Если обозначить , то и из уравнения (6) получаем

Или . (7)

Поскольку уравнение (7) имеет вид , то это уравнение равносильно неравенству . Отсюда получаем . Так как , то или .

Ответ: .

Пример 10. Решить уравнение . (8)

Решение. Согласно теореме 1 можно записать

(9)

Принимая во внимание уравнение (8), делаем вывод о том, что оба неравенства (9) обращаются в равенства, т.е. имеет место система уравнений

Однако по теореме 3 приведенная выше система уравнений равносильна системе неравенств

(10)

Решая систему неравенств (10) получаем . Так как система неравенств (10) равносильна уравнению (8), то исходное уравнение имеет единственный корень .

Ответ: .

Пример 11. Решить уравнение . (11)

Решение. Пусть и , тогда из уравнения (11) вытекает равенство .

Отсюда следует, что и . Таким образом, здесь имеем систему неравенств

Решением данной системы неравенств являются и .

Ответ: , .

Пример 12. Решить уравнение . (12)

Решение. Уравнение (12) будем решать методом последовательного раскрытия модулей. Для этого рассмотрим несколько случаев.

1. Если , то .

1.1. Если , то и , .

1.2. Если , то . Однако , поэтому в данном случае уравнение (12) корней не имеет.

2. Если , то .

2.1. Если , то и , .

2.2. Если , то и .

Ответ: , , , , .

Пример 13. Решить уравнение . (13)

Решение. Поскольку левая часть уравнения (13) неотрицательна, то и . В этой связи , и уравнение (13)

принимает вид или .

Известно , что уравнение равносильно совокупности двух уравнений и , решая которые получаем , . Так как , то уравнение (13) имеет один корень .

Ответ: .

Пример 14. Решить систему уравнений (14)

Решение. Так как и , то и . Следовательно, из системы уравнений (14) получаем четыре системы уравнений:

Корни приведенных выше систем уравнений являются корнями системы уравнений (14).

Ответ: ,, , , , , , .

Пример 15. Решить систему уравнений (15)

Решение. Так как , то . В этой связи из системы уравнений (15) получаем две системы уравнений

Корнями первой системы уравнений являются и , а из второй системы уравнений получаем и .

Ответ: , , , .

Пример 16. Решить систему уравнений (16)

Решение. Из первого уравнения системы (16) следует, что .

Так как , то . Рассмотрим второе уравнение системы. Поскольку , то , и уравнение принимает вид , , или .

Если подставить значение в первое уравнение системы (16) , то , или .

Ответ: , .

Для более глубокого изучения методов решения задач , связанных с решением уравнений , содержащих переменные под знаком модуля , можно посоветовать учебные пособия из списка рекомендуемой литературы.

1. Сборник задач по математике для поступающих во втузы / Под ред. М.И. Сканави. – М.: Мир и Образование , 2013. – 608 с.

2. Супрун В.П. Математика для старшеклассников: задачи повышенной сложности. – М.: КД «Либроком» / URSS , 2017. – 200 с.

3. Супрун В.П. Математика для старшеклассников: нестандартные методы решения задач. – М.: КД «Либроком» / URSS , 2017. – 296 с.

Остались вопросы?

Чтобы получить помощь репетитора – зарегистрируйтесь .

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

В этой статье мы детально разберем модуль числа . Мы дадим различные определения модуля числа, введем обозначения и приведем графические иллюстрации. При этом рассмотрим различные примеры нахождения модуля числа по определению. После этого мы перечислим и обоснуем основные свойства модуля. В конце статьи поговорим о том, как определяется и находится модуль комплексного числа.

Навигация по странице.

Модуль числа – определение, обозначение и примеры

Сначала введем обозначение модуля числа . Модуль числа a будем записывать как , то есть, слева и справа от числа будем ставить вертикальные черточки, образующие знак модуля. Приведем пару примеров. Например, модуль −7 можно записать как ; модуль 4,125 записывается как , а модуль имеет запись вида .

Следующее определение модуля относится к , а следовательно, и к , и к целым, и к рациональным, и к иррациональным числам, как к составляющим частям множества действительных чисел. О модуле комплексного числа мы поговорим в .

Определение.

Модуль числа a – это либо само число a , если a – положительное число, либо число −a , противоположное числу a , если a – отрицательное число, либо 0 , если a=0 .

Озвученное определение модуля числа часто записывают в следующем виде , эта запись означает, что , если a>0 , , если a=0 , и , если a<0 .

Запись можно представить в более компактной форме . Эта запись означает, что , если (a больше или равно 0 ), и , если a<0 .

Также имеет место и запись . Здесь отдельно следует пояснить случай, когда a=0 . В этом случае имеем , но −0=0 , так как нуль считают числом, которое противоположно самому себе.

Приведем примеры нахождения модуля числа с помощью озвученного определения. Для примера найдем модули чисел 15 и . Начнем с нахождения . Так как число 15 – положительное, то его модуль по определению равен самому этому числу, то есть, . А чему равен модуль числа ? Так как - отрицательное число, то его модуль равен числу, противоположному числу , то есть, числу . Таким образом, .

В заключение этого пункта приведем один вывод, который очень удобно применять на практике при нахождении модуля числа. Из определения модуля числа следует, что модуль числа равен числу под знаком модуля без учета его знака , а из рассмотренных выше примеров это очень отчетливо видно. Озвученное утверждение объясняет, почему модуль числа называют еще абсолютной величиной числа . Так модуль числа и абсолютная величина числа – это одно и то же.

Модуль числа как расстояние

Геометрически модуль числа можно интерпретировать как расстояние . Приведем определение модуля числа через расстояние .

Определение.

Модуль числа a – это расстояние от начала отсчета на координатной прямой до точки, соответствующей числу a.

Данное определение согласуется с определением модуля числа, данного в первом пункте. Поясним этот момент. Расстояние от начала отсчета до точки, которой соответствует положительное число, равно этому числу. Нулю соответствует начало отсчета, поэтому расстояние от начала отсчета до точки с координатой 0 равно нулю (не нужно откладывать ни одного единичного отрезка и ни одного отрезка, составляющего какую-нибудь долю единичного отрезка, чтобы от точки O попасть в точку с координатой 0 ). Расстояние от начала отсчета до точки с отрицательной координатой равно числу, противоположному координате данной точки, так как равно расстоянию от начала координат до точки, координатой которой является противоположное число.

Например, модуль числа 9 равен 9 , так как расстояние от начала отсчета до точки с координатой 9 равно девяти. Приведем еще пример. Точка с координатой −3,25 находится от точки O на расстоянии 3,25 , поэтому .

Озвученное определение модуля числа является частным случаем определения модуля разности двух чисел.

Определение.

Модуль разности двух чисел a и b равен расстоянию между точками координатной прямой с координатами a и b .

То есть, если даны точки на координатной прямой A(a) и B(b) , то расстояние от точки A до точки B равно модулю разности чисел a и b . Если в качестве точки В взять точку O (начало отсчета), то мы получим определение модуля числа, приведенное в начале этого пункта.

Определение модуля числа через арифметический квадратный корень

Иногда встречается определение модуля через арифметический квадратный корень .

Для примера вычислим модули чисел −30 и на основании данного определения. Имеем . Аналогично вычисляем модуль двух третьих: .

Определение модуля числа через арифметический квадратный корень также согласуется с определением, данным в первом пункте этой статьи. Покажем это. Пусть a – положительное число, при этом число −a – отрицательное. Тогда и , если же a=0 , то .

Свойства модуля

Модулю присущ ряд характерных результатов - свойства модуля . Сейчас мы приведем основные и наиболее часто используемые из них. При обосновании этих свойств мы будем опираться на определение модуля числа через расстояние.

Начнем с самого очевидного свойства модуля – модуль числа не может быть отрицательным числом . В буквенном виде это свойство имеет запись вида для любого числа a . Это свойство очень легко обосновать: модуль числа есть расстояние, а расстояние не может выражаться отрицательным числом.

Переходим к следующему свойству модуля. Модуль числа равен нулю тогда и только тогда, когда это число есть нуль . Модуль нуля есть нуль по определению. Нулю соответствует начало отсчета, никакая другая точка на координатной прямой нулю не соответствует, так как каждому действительному числу поставлена в соответствие единственная точка на координатной прямой. По этой же причине любому числу, отличному от нуля, соответствует точка, отличная от начала отсчета. А расстояние от начала отсчета до любой точки, отличной от точки O , не равно нулю, так как расстояние между двумя точками равно нулю тогда и только тогда, когда эти точки совпадают. Приведенные рассуждения доказывают, что нулю равен лишь модуль нуля.

Идем дальше. Противоположные числа имеют равные модули, то есть, для любого числа a . Действительно, две точки на координатной прямой, координатами которых являются противоположные числа, находятся на одинаковом расстоянии от начала отсчета, значит модули противоположных чисел равны.

Следующее свойство модуля таково: модуль произведения двух чисел равен произведению модулей этих чисел , то есть, . По определению модуль произведения чисел a и b равен либо a·b , если , либо −(a·b) , если . Из правил умножения действительных чисел следует, что произведение модулей чисел a и b равно либо a·b , , либо −(a·b) , если , что доказывает рассматриваемое свойство.

Модуль частного от деления a на b равен частному от деления модуля числа a на модуль числа b , то есть, . Обоснуем это свойство модуля. Так как частное равно произведению , то . В силу предыдущего свойства имеем . Осталось лишь воспользоваться равенством , которое справедливо в силу определения модуля числа.

Следующее свойство модуля записывается в виде неравенства: , a , b и c – произвольные действительные числа. Записанное неравенство представляет собой ни что иное как неравенство треугольника . Чтобы это стало понятно, возьмем точки A(a) , B(b) , C(c) на координатной прямой, и рассмотрим вырожденный треугольник АВС , у которого вершины лежат на одной прямой. По определению модуля разности равен длине отрезка АВ , - длине отрезка АС , а - длине отрезка СВ . Так как длина любой стороны треугольника не превосходит сумму длин двух других сторон, то справедливо неравенство , следовательно, справедливо и неравенство .

Только что доказанное неравенство намного чаще встречается в виде . Записанное неравенство обычно рассматривают как отдельное свойство модуля с формулировкой: «Модуль суммы двух чисел не превосходит сумму модулей этих чисел ». Но неравенство напрямую следует из неравенства , если в нем вместо b положить −b , и принять c=0 .

Модуль комплексного числа

Дадим определение модуля комплексного числа . Пусть нам дано комплексное число , записанное в алгебраической форме , где x и y – некоторые действительные числа, представляющие собой соответственно действительную и мнимую части данного комплексного числа z , а – мнимая единица.

МБОУ СОШ №17 г. Иванова

«Уравнения с модулем»
Методическая разработка

Составлена

учителем математики

Лебедевой Н.В.

20010 г.

Пояснительная записка

Глава 1. Введение

Раздел 2. Основные свойства Раздел 3. Геометрическая интерпретация понятия модуля числа Раздел 4. График функции у = |х| Раздел 5. Условные обозначения

Глава 2. Решение уравнений, содержащих модуль

Раздел 1.Уравнения вида |F(х)| = m (простейшие) Раздел 2. Уравнения вида F(|х|) = m Раздел 3. Уравнения вида |F(х)| = G(х) Раздел 4. Уравнения вида |F(х)| = ± F(х) (красивейшие) Раздел 5. Уравнения вида |F(х)| = |G(х)| Раздел 6. Примеры решения нестандартных уравнений Раздел 7. Уравнения вида |F(х)| + |G(х)| = 0 Раздел 8. Уравнения вида |а 1 х ± в 1 | ± |а 2 х ± в 2 | ± …|а n х ± в n | = m Раздел 9. Уравнения, содержащие несколько модулей

Глава 3. Примеры решения различных уравнений с модулем.

Раздел 1. Тригонометрические уравнения Раздел 2. Показательные уравнения Раздел 3. Логарифмические уравнения Раздел 4. Иррациональные уравнения Раздел 5. Задания повышенной сложности Ответы к упражнениям Список литературы

Пояснительная записка.

Понятие абсолютной величины (модуля) действительного числа является одной из существенных его характеристик. Это понятие имеет широкое распространение в различных разделах физико-математических и технических наук. В практике преподавания курса математики в средней школе в соответствии с Программой МО РФ понятие «абсолютная величина числа» встречается неоднократно: в 6 – м классе вводиться определение модуля, его геометрический смысл; в 8 – м классе формируется понятие абсолютной погрешности, рассматривается решение простейших уравнений и неравенств, содержащих модуль, изучаются свойства арифметического квадратного корня; в 11 – м классе понятие встречается в разделе «Корень n -ой степени». Опыт преподавания показывает, что учащиеся часто сталкиваются с трудностями при решении заданий, требующих знания данного материала, а нередко пропускают, не приступая к выполнению. В текстах экзаменационных заданий за курс 9 – ого и 11 – ого классов также включены подобные задания. Кроме того, требования, которые предъявляют к выпускникам школ Вузы отличаются, а именно, более высокого уровня, чем требования школьной программы. Для жизни в современном обществе очень важным является формирование математического стиля мышления, проявляющегося в определённых умственных навыках. В процессе решения задач с модулями требуется умение применять такие приёмы, как обобщение и конкретизация, анализ, классификация и систематизация, аналогия. Решение подобных заданий позволяет проверить знание основных разделов школьного курса, уровень логического мышления, первоначальные навыки исследовательской деятельности. Данная работа посвящена одному из разделов – решению уравнений, содержащих модуль. Она состоит из трёх глав. В первой главе вводятся основные понятия и наиболее важные теоретические выкладки. Во второй главе предлагаются девять основных типов уравнений, содержащих модуль, рассматриваются методы их решения, разбираются примеры разного уровня сложности. В третьей главе предлагаются более сложные и нестандартные уравнения (тригонометрические, показательные, логарифмические и иррациональные). К каждому типу уравнений есть упражнения для самостоятельного решения (ответы и указания прилагаются). Основное назначение данной работы – это оказание методической помощи преподавателям при подготовке к урокам и при организации факультативных курсов. Материал также может быть использован в качестве учебного пособия для старшеклассников. Задания, предлагаемые в работе, интересны и не всегда просты в решении, что позволяет сделать учебную мотивацию учащихся более осознанной, проверить свои способности, повысить уровень подготовки выпускников школ к поступлению в Вузы. Дифференцированный подбор предлагаемых упражнений предполагает переход от репродуктивного уровня усвоения материала к творческому, а также возможность научить применять свои знания при решении нестандартных задач.

Глава 1. Введение.

Раздел 1. Определение абсолютной величины .

Определение : Абсолютной величиной (модулем) действительного числа а называется неотрицательное число: а или –а. Обозначение: │ а │ Запись читается следующим образом: «модуль числа а» или «абсолютная величина числа а»

│ а, если а > 0

│а│ = │ 0, если а = 0 (1)

│ - а, если а
Примеры: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1

Раскрыть модуль выражения:

а) │х - 8│, если х > 12 б) │2х + 3│, если х ≤ -2 │х – 8│= х – 8 │ 2х + 3│= - 2х – 3

Раздел 2. Основные свойства.

Рассмотрим основные свойства абсолютной величины. Свойство №1: Противоположные числа имеют равные модули, т.е. │а│=│- а│ Покажем верность равенства. Запишем определение числа – а : │- а│ = (2) Сравним совокупности (1) и (2). Очевидно, что определения абсолютных величин чисел а и – а совпадают. Следовательно, │а│=│- а│
При рассмотрении следующих свойств ограничимся их формулировкой, так как их доказательство приводится в Свойство №2: Абсолютная величина суммы конечного числа действительных чисел не превосходит суммы абсолютных величин слагаемых: │а 1 + а 2 +…+ а n │ ≤│а 1 │+│а 2 │+ … + │а n │ Свойство №3: Абсолютная величина разности двух действительных чисел не превосходит суммы их абсолютных величин: │а - в│ ≤│а│+│в│ Свойство №4: Абсолютная величина произведения конечного числа действительных чисел равна произведению абсолютных величин множителей: │а · в│=│а│·│в│ Свойство №5: Абсолютная величина частного действительных чисел равна частному их абсолютных величин:

Раздел 3. Геометрическая интерпретация понятия модуля числа.

Каждому действительному числу можно поставить в соответствие точку на числовой прямой, которая будет геометрическим изображением данного действительного числа. Каждой точке на числовой прямой соответствует её расстояние от начала отсчёта, т.е. длина отрезка от начала отсчёта до данной точки. Это расстояние рассматривается всегда как величина неотрицательная. Поэтому длина соответствующего отрезка и будет геометрической интерпретацией абсолютной величины данного действительного числа

Представленная геометрическая иллюстрация наглядно подтверждает свойство №1, т.е. модули противоположных чисел равны. Отсюда легко понимается справедливость равенства: │х – а│= │а - х│. Также более очевидным становиться решение уравнения │х│= m, где m ≥ 0, а именно х 1,2 = ± m. Примеры: 1) │х│= 4 х 1,2 = ± 4 2) │х - 3│= 1
х 1,2 = 2; 4

Раздел 4. График функции у = │х│

Область определения данной функции все действительные числа.

Раздел 5. Условные обозначения.

В дальнейшем при рассмотрении примеров решения уравнений будут использованы следующие условные обозначения: { - знак системы [ - знак совокупности При решение системы уравнений (неравенств) находится пересечение решений входящих в систему уравнений (неравенств). При решении совокупности уравнений (неравенств) находится объединение решений входящих в совокупность уравнений (неравенств).

Глава 2. Решение уравнений, содержащих модуль.

В этой главе мы рассмотрим алгебраические способы решения уравнений, содержащих один или более модуль.

Раздел 1. Уравнения вида │F (х)│= m

Уравнение данного вида называется простейшим. Оно имеет решение тогда и только тогда, когда m ≥ 0. По определению модуля, исходное уравнение равносильно совокупности двух уравнений: │F (х)│= m
Примеры:
№1. Решите уравнение: │7х - 2│= 9


Ответ: х 1 = - 1; х 2 = 1 4 / 7 №2
│х 2 + 3х + 1│= 1

х 2 + 3х + 2 = 0 х 2 +3х = 0 х 1 = -1; х 2 = -2 х · (х + 3) = 0 х 1 = 0; х 2 = -3 Ответ: сумма корней равна - 2 .№3
│х 4 -5х 2 + 2│= 2 х 4 – 5х 2 = 0 х 4 – 5х 2 + 4 = 0 х 2 · (х 2 – 5) = 0 обозначим х 2 = m, m ≥ 0 х = 0; ±√5 m 2 – 5m + 4 = 0 m = 1; 4 – оба значения удовлетворяют условию m ≥ 0 х 2 = 1 х 2 = 4 х = ± 1 х = ± 2 Ответ: количество корней уравнения 7. Упражнения:
№1. Решите уравнение и укажите сумму корней: │х - 5│= 3№2 . Решите уравнение и укажите меньший корень: │х 2 + х│= 0№3 . Решите уравнение и укажите больший корень: │х 2 – 5х + 4│= 4№4 .Решите уравнение и укажите целый корень: │2х 2 – 7х + 6│= 1№5 .Решите уравнение и укажите количество корней: │х 4 – 13х 2 + 50│= 14

Раздел 2. Уравнения вида F(│х│) = m

Аргумент функции в левой части находится под знаком модуля, а правая часть не зависит от переменной. Рассмотрим два способа решения уравнений данного вида.1 способ: По определению абсолютной величины исходное уравнение равносильно совокупности двух систем. В каждой из которых накладывается условие на подмодульное выражение. F (│х│) = m
Так как функция F(│х│) – чётная на всей области определения, то корни уравнений F(х) = m и F(- х) = m – это пары противоположных чисел. Поэтому достаточно решить одну из систем (при рассмотрении примеров указанным способом будет приводиться решение одной системы).2 способ: Применение метода введения новой переменной. При этом вводиться обозначение │х│= а, где а ≥ 0. Данный способ менее объёмный по оформлению.
Примеры: №1 . Решите уравнение: 3х 2 – 4│х│= - 1 Воспользуемся введением новой переменной. Обозначим │х│= а, где а ≥ 0. Получим уравнение 3а 2 - 4а + 1 = 0 Д = 16 – 12 = 4 а 1 = 1 а 2 = 1 / 3 Возвращаемся к исходной переменной: │х│=1 и │х│= 1 / 3 . Каждое уравнение имеет два корня. Ответ: х 1 = 1; х 2 = - 1; х 3 = 1 / 3 ; х 4 = - 1 / 3 . №2. Решите уравнение: 5х 2 + 3│х│- 1 = 1 / 2 │х│ + 3х 2
Найдём решение первой системы совокупности: 4х 2 + 5х – 2 =0 Д = 57 х 1 = -5+√57 / 8 х 2 = -5-√57 / 8 Заметим, что х 2 не удовлетворяет условию х ≥ 0. Решением второй системы будет число, противоположное значению х 1 . Ответ: х 1 = -5+√57 / 8 ; х 2 = 5-√57 / 8 .№3 . Решите уравнение: х 4 – │х│= 0 Обозначим │х│= а, где а ≥ 0. Получим уравнение а 4 – а = 0 а · (а 3 – 1) = 0 а 1 = 0 а 2 = 1 Возвращаемся к исходной переменной: │х│=0 и │х│= 1 х = 0; ± 1 Ответ: х 1 = 0; х 2 = 1; х 3 = - 1.
Упражнения: №6. Решите уравнение: 2│х│ - 4,5 = 5 – 3 / 8 │х│ №7 . Решите уравнение, в ответе укажите количество корней: 3х 2 - 7│х│ + 2 = 0 №8 . Решите уравнение, в ответе укажите целые решения: х 4 + │х│ - 2 = 0

Раздел 3. Уравнения вида │F(х)│ = G(х)

Правая часть уравнения данного вида зависит от переменной и, следовательно, имеет решение тогда и только тогда, когда правая часть функция G(х) ≥ 0. Исходное уравнение можно решить двумя способами:1 способ: Стандартный, основан на раскрытии модуля исходя из его определения и заключается в равносильном переходе к совокупности двух систем. │F (х)│ = G (х)

Данный способ рационально использовать в случае сложного выражения для функции G(x) и мене сложного – для функции F(х), так как предполагается решение неравенств с функцией F(х).2 способ: Состоит в переходе к равносильной системе, в которой накладывается условие на правую часть. │F (x )│= G (x )

Данный способ удобнее применять, если выражение для функции G(х) мене сложное, чем для функции F(х), так как предполагается решение неравенства G(х) ≥ 0. Кроме того, в случае нескольких модулей этот способ рекомендуется применять второй вариант. Примеры: №1. Решите уравнение: │х + 2│= 6 -2х
(1 способ) Ответ: х = 1 1 / 3 №2.
│х 2 – 2х - 1│= 2·(х + 1)
(2 способ) Ответ: Произведение корней – 3.
№3. Решите уравнение,в ответе укажите сумму корней:
│х - 6│= х 2 - 5х + 9

Ответ: сумма корней равна 4.
Упражнения: №9. │х + 4│= - 3х№10. Решите уравнение, в ответе укажите число решений:│х 2 + х - 1│= 2х – 1№11 . Решите уравнение, в ответе укажите произведение корней:│х + 3│= х 2 + х – 6

Раздел 4. Уравнения вида │F(x)│= F(x) и │F(x)│= - F(x)

Уравнения данного вида иногда называют «красивейшими». Так как правая часть уравнений зависит от переменной, решения существуют тогда и только тогда, когда правая часть неотрицательна. Поэтому исходные уравнения равносильны неравенствам:
│F(x)│= F(x) F(x) ≥ 0 и │F(x)│= - F(x) F(x) Примеры: №1 . Решите уравнение, в ответе укажите меньший целый корень: │5х - 3│= 5х – 3 5х – 3 ≥ 0 5х ≥ 3 х ≥ 0,6 Ответ: х = 1 №2. Решите уравнение, в ответе укажите длину промежутка: │х 2 - 9│= 9 – х 2 х 2 – 9 ≤ 0 (х – 3) (х + 3) ≤ 0 [- 3; 3] Ответ: длина промежутка равна 6. №3 . Решите уравнение, в ответе укажите число целых решений: │2 + х – х 2 │= 2 + х – х 2 2 + х – х 2 ≥ 0 х 2 – х – 2 ≤ 0 [- 1; 2] Ответ: 4 целых решения. №4 . Решите уравнение, в ответе укажите наибольший корень:
│4 – х -
│= 4 – х –
х 2 – 5х + 5 = 0 Д = 5 х 1,2 =
≈ 1,4

Ответ: х = 3.

Упражнения: №12. Решите уравнение, в ответе укажите целый корень: │х 2 + 6х + 8│= х 2 + 6х + 8№13. Решите уравнение, в ответе укажите число целых решений: │13х – х 2 - 36│+ х 2 – 13х + 36 = 0№14. Решите уравнение, в ответе укажите целое число, не являющееся корнем уравнения:

Раздел 5. Уравнения вида │F(x)│= │G(x)│

Так как обе части уравнения неотрицательные, то решение предполагает рассмотрение двух случаев: подмодульные выражения равны или противоположны по знаку. Следовательно, исходное уравнение равносильно совокупности двух уравнений: │F (x )│= │ G (x )│
Примеры: №1. Решите уравнение, в ответе укажите целый корень: │х + 3│=│2х - 1│
Ответ: целый корень х = 4. №2. Решите уравнение: │ х – х 2 - 1│=│2х – 3 – х 2 │
Ответ: х = 2. №3 . Решите уравнение, в ответе укажите произведение корней:




Корниуравнения 4х 2 + 2х – 1 = 0 х 1,2 = - 1±√5 / 4 Ответ: произведение корней равно – 0,25. Упражнения: №15 . Решите уравнение, в ответе укажите целое решение:│х 2 – 3х + 2│= │х 2 + 6х - 1│ №16. Решите уравнение, в ответе укажите меньший корень:│5х - 3│=│7 - х│ №17 . Решите уравнение, в ответе укажите сумму корней:

Раздел 6. Примеры решения нестандартных уравнений

В данном разделе мы рассмотрим примеры нестандартных уравнений, при решении которых абсолютная величина выражения раскрывается по определению. Примеры:

№1. Решите уравнение, в ответе укажите сумму корней: х · │х│- 5х – 6 = 0
Ответ: сумма корней равна 1 №2. . Решите уравнение, в ответе укажите меньший корень: х 2 - 4х ·
- 5 = 0
Ответ: меньший корень х = - 5. №3. Решите уравнение:

Ответ: х = -1. Упражнения: №18. Решите уравнение и укажите сумму корней: х · │3х + 5│= 3х 2 + 4х + 3
№19. Решите уравнение: х 2 – 3х =

№20. Решите уравнение:

Раздел 7. Уравнения вида │F(x)│+│G(x)│=0

Нетрудно заметить, что в левой части уравнения данного вида сумма неотрицательных величин. Следовательно, исходное уравнение имеет решение тогда и только тогда, когда оба слагаемых одновременно равны нулю. Уравнение равносильно системе уравнений: │F (x )│+│ G (x )│=0
Примеры: №1 . Решите уравнение:
Ответ: х = 2. №2. Решите уравнение: Ответ: х = 1. Упражнения: №21. Решите уравнение: №22 . Решите уравнение, в ответе укажите сумму корней: №23 . Решите уравнение, в ответе укажите количество решений:

Раздел 8. Уравнения вида │а 1 х + в 1 │±│а 2 х + в 2 │± … │а n х +в n │= m

Для решения уравнений данного вида применяется метод интервалов. Если его решать последовательным раскрытием модулей, то получим n совокупностей систем, что очень громоздко и неудобно. Рассмотрим алгоритм метода интервалов: 1). Найти значения переменной х , при которых каждый модуль равен нулю (нули подмодульных выражений):
2). Найденные значения отметить на числовой прямой, которая разбивается на интервалы (количество интервалов соответственно равно n +1 ) 3). Определить, с каким знаком раскрывается каждый модуль на каждом из полученных интервалов (при оформлении решения можно использовать числовую прямую, отметив на ней знаки) 4). Исходное уравнение равносильно совокупности n +1 систем, в каждой из которых указывается принадлежность переменной х одному из интервалов. Примеры: №1 . Решите уравнение, в ответе укажите наибольший корень:
1). Найдём нули подмодульных выражений: х = 2; х = -3 2). Отметим найденные значения на числовой прямой и определим, с каким знаком раскрывается каждый модуль на полученных интервалах:
х – 2 х – 2 х – 2 - - + - 3 2 х 2х + 6 2х + 6 2х + 6 - + + 3)
- нет решений Уравнение имеет два корня. Ответ: наибольший корень х = 2. №2. Решите уравнение, в ответе укажите целый корень:
1). Найдём нули подмодульных выражений: х = 1,5; х = - 1 2). Отметим найденные значения на числовой прямой и определим, с каким знаком раскрывается каждый модуль на полученных интервалах: х + 1 х + 1 х + 1 - + +
-1 1,5 х 2х – 3 2х – 3 2х – 3 - - +
3).
Последняя система не имеет решений, следовательно, уравнение имеет два корня. В ходе решения уравнения следует обратить внимание на знак « - » перед вторым модулем. Ответ: целый корень х = 7. №3. Решите уравнение, в ответе укажите сумму корней: 1). Найдём нули подмодульных выражений: х = 5; х = 1; х = - 2 2). Отметим найденные значения на числовой прямой и определим, с каким знаком раскрывается каждый модуль на полученных интервалах: х – 5 х – 5 х – 5 х – 5 - - - +
-2 1 5 х х – 1 х – 1 х – 1 х – 1 - - + + х + 2 х + 2 х + 2 х + 2 - + + +
3).
Уравнение имеет два корня х = 0 и 2. Ответ: сумма корней равна 2. №4 . Решите уравнение: 1). Найдём нули подмодульных выражений: х = 1; х = 2; х = 3. 2). Определим, с каким знаком раскрывается каждый модуль на полученных интервалах. 3).
Объединим решения первых трёх систем. Ответ: ; х = 5.
Упражнения: №24. Решите уравнение:
№25. Решите уравнение, в ответе укажите сумму корней: №26. Решите уравнение, в ответе укажите меньший корень:№27. Решите уравнение, в ответе укажите больший корень:

Раздел 9. Уравнения, содержащие несколько модулей

Уравнения, содержащие несколько модулей, предполагают наличие абсолютных величин в подмодульных выражениях. Основной принцип решения уравнений данного вида – это последовательное раскрытие модулей, начиная с «внешнего». В ходе решения используются приёмы, рассмотренные в разделах №1, №3.

Примеры: №1. Решите уравнение:
Ответ: х = 1; - 11. №2. Решите уравнение:
Ответ: х = 0; 4; - 4. №3. Решите уравнение, в ответе укажите произведение корней:
Ответ: произведение корней равно – 8. №4. Решите уравнение:
Обозначим уравнения совокупности (1) и (2) и рассмотрим решение каждого из них отдельно для удобства оформления. Так как оба уравнения содержат более одного модуля, то удобнее осуществить равносильный переход к совокупностям систем.(1)

(2)


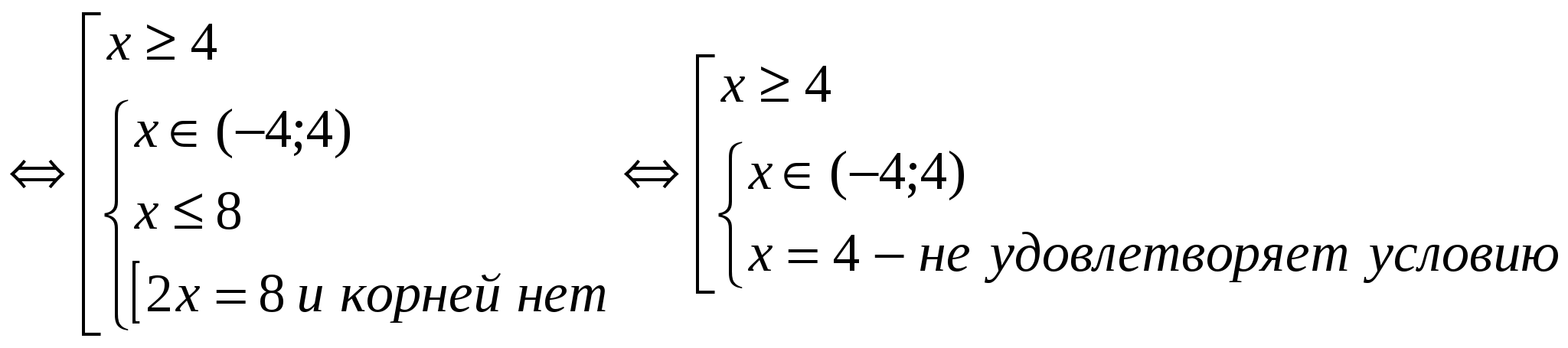Ответ:
Упражнения: №36. Решите уравнение, в ответе укажите сумму корней: 5 │3х-5│ = 25 х №37. Решите уравнение, если корней более одного, в ответе укажите сумму корней: │х + 2│ х – 3х – 10 = 1 №38. Решите уравнение: 3 │2х -4│ = 9 │х│ №39. Решите уравнение, в ответе укажите количество корней на : 2 │ sin х│ = √2 №40 . Решите уравнение, в ответе укажите количество корней:

Раздел 3. Логарифмические уравнения.

Перед решением следующих уравнений необходимо повторить свойства логарифмов и логарифмической функции. Примеры: №1. Решите уравнение, в ответе укажите произведение корней: log 2 (х+1) 2 + log 2 │x+1│ = 6 О.Д.З. х+1≠0 х≠ - 1

1 случай: если х ≥ - 1, то log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – удовлетворяет условию х ≥ - 1 2 случай: если х log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – удовлетворяет условию х - 1
Ответ: произведение корней равно – 15.
№2. Решите уравнение, в ответе укажите сумму корней: lg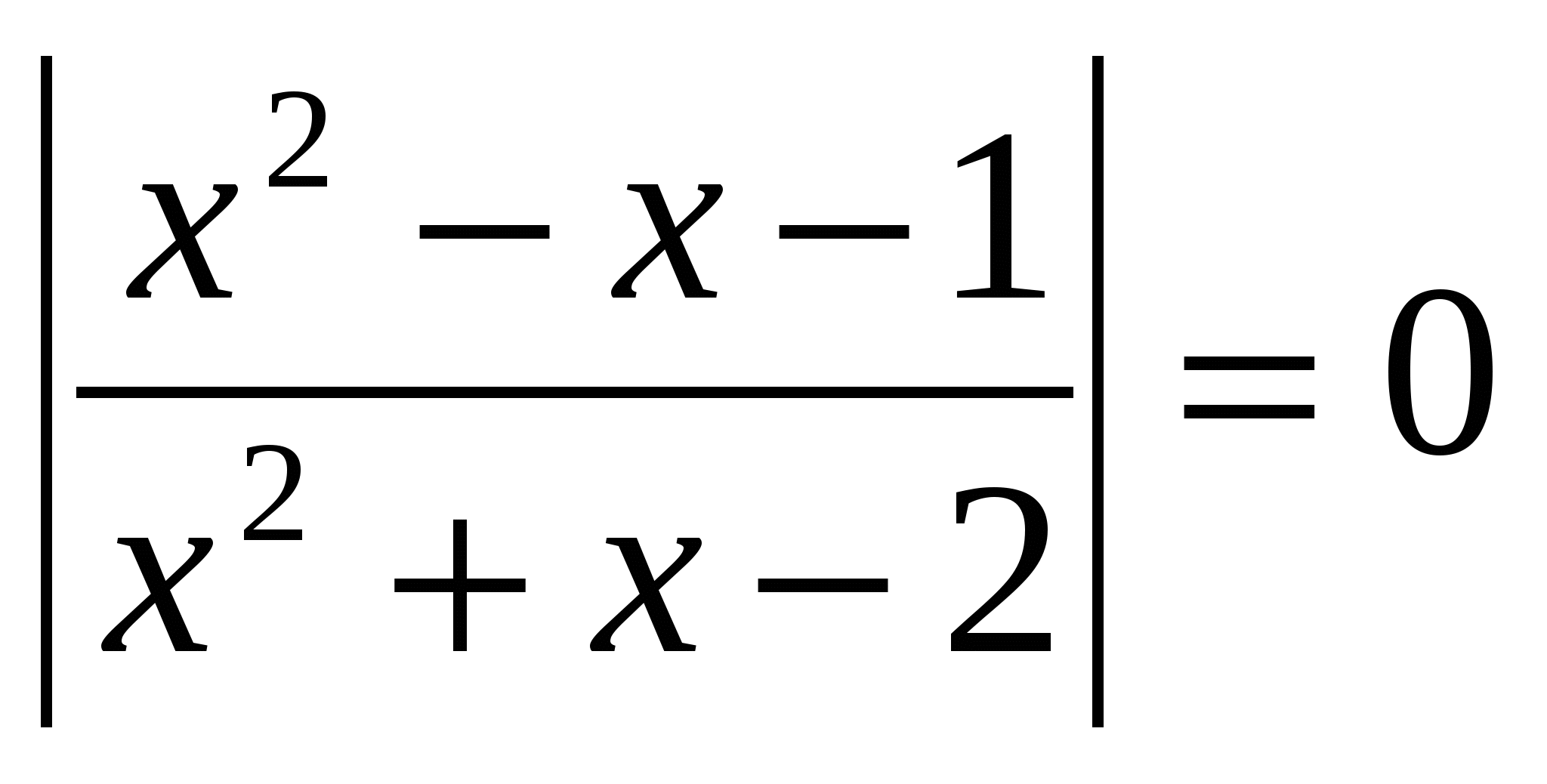
О.Д.З.

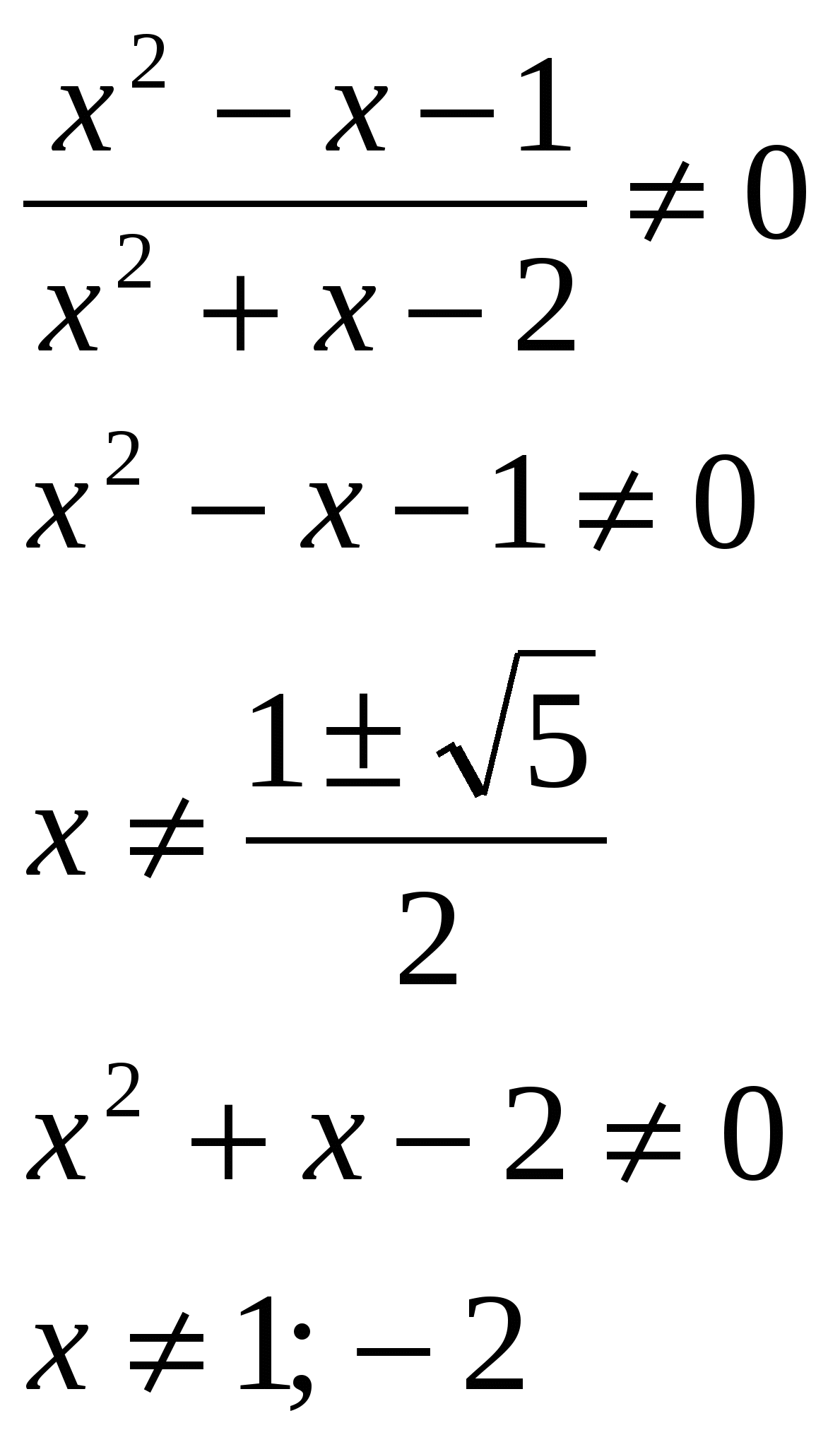
Ответ: сумма корней равна 0,5.
№3. Решите уравнение: log 5
О.Д.З.

Ответ: х = 9. №4. Решите уравнение: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ О.Д.З. х > 0 Воспользуемся формулой перехода к другому основанию. │2 - log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Найдём нули подмодульных выражений: х = 25; х = Эти числа делят область допустимых значений на три интервала, поэтому уравнение равносильно совокупности трёх систем.
Ответ: }